2.1 - Algorithms (Part 2)

Inputs, outputs and processes for a problem

- Thinking algorithmically allows you to come up with a list of step-by-step instructions to solve a problem.
- You need to be able to identify inputs, outputs and processes.

Inputs

- Inputs are the data that you need to solve a problem.
- For example, if you were to solve the problem of finding the largest number in a list, you would need to know the list of numbers to find the largest number in.
- Input can come from places like the user, or from a file, or from a database, or from a network, or from sensors, or anything else you can think of.

Outputs

- Outputs are the result of the processing of the inputs through the algorithm.
- Continuing with the example, you would need to output the solution at the end of processing.
- Outputs can take forms such as text, numbers, images, sounds, or even trigger events.

Processes

- Processes are the steps that the algorithm takes to solve the problem.
- With the example of finding the largest number in a list, you would need to compare each number in the list, and if the current number is larger than the previous largest number, replace the previous largest number with the current number.
- Processes can be as simple as a single line of code, or as complex as a whole program.

Structure Diagrams

- Structure diagrams are a visual representation of decomposition of a problem.
- They are also used to show the relationship between inputs, outputs and processes, and to show the flow of data through the algorithm.

Pseudocode

- Occassionally in an exam you will be asked to write your answer in pseudocode, or read pseudocode.
- Pseudocode is a way of writing code that is not meant to be executed, but rather to show the logic of the code.
- For exams you should learn the OCR Exam Reference Language, which is a form of pseudocode.
- This document explains it quite well, so I won't rewrite it all here (the doc is from 2015 but it's not like it's changed much since then).

Flowcharts

- Flowcharts are a visual representation of the steps in a process.
- They are also used to show the flow of data through the algorithm.
- They use different symbols to represent what goes on in each step:

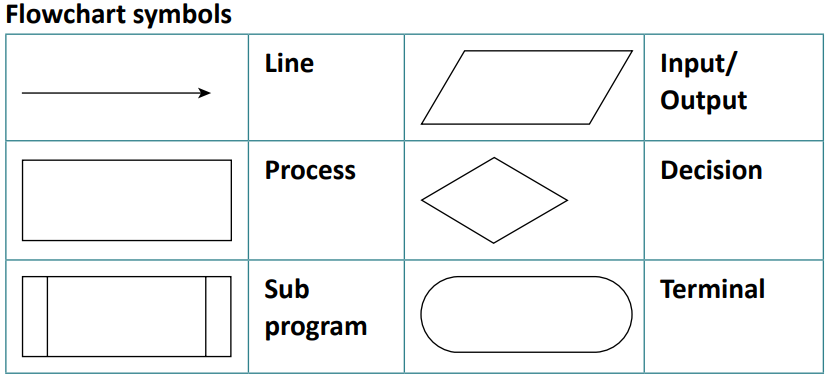
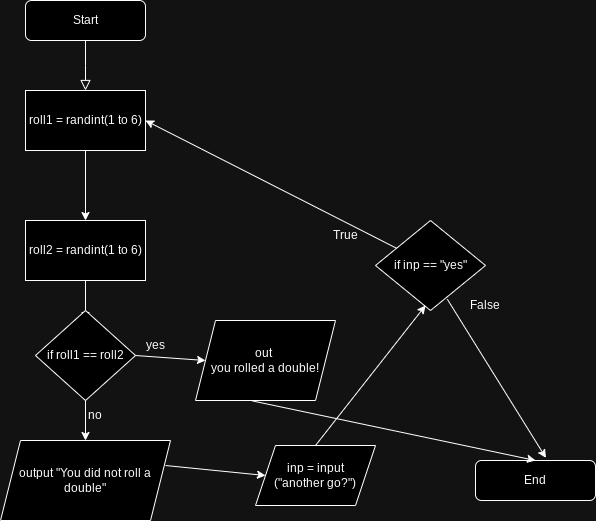
- Here is an example flowchart for a dice game:

Identifying Common Errors

note: due to the amount of large tables this content is better viewed on a PC from here until the end of the page

- You need to be able to identify common errors in your code.
- This helps with both debugging and understanding the logic of the code.
- Common errors include:

• Syntax errors
• Logical errors
• Runtime errors

Syntax Errors

- Syntax errors are errors in the structure of the code.
- They are usually easy to spot, as they will cause the code to not run at all.
- Examples of syntax errors include:

• Missing a closing bracket
• Using a variable that hasn't been declared
• Using a variable before it has been declared
• Using a variable in the wrong place

Logical Errors

- Logical errors occur when the code runs but produces incorrect results.
- These errors can be harder to identify because the program does not crash.
- Examples of logical errors include:

• Incorrect use of conditions in an if statement
• Loops that iterate too many or too few times
• Off-by-one errors, such as starting a loop at 1 instead of 0
• Using the wrong mathematical operator in a calculation

Runtime Errors

- Runtime errors occur when the code is executed, leading to crashes or unexpected behavior.
- These errors happen after the code has successfully passed syntax checks and started running.
- Examples of runtime errors include:

• Dividing a number by zero
• Accessing an index that is out of range in an array
• Running out of memory due to excessive memory allocation
• File not found errors when trying to open a non-existent file

Examples of Code Errors and Corrections

// Missing closing bracket
function calculate_area(radius)
    area = 3.14 * radius ** 2
    print("Area is: ", area
endfunction

// Corrected by adding the closing bracket
function calculate_area(radius)
    area = 3.14 * radius ** 2
    print("Area is: ", area)
endfunction

// Incorrect condition in the if statement
// ('=' is only for assignment)
function check_even(number)
    if number % 2 = 0:
        print("Even number")
    else:
        print("Odd number")
endfunction

// Corrected condition in the if statement
function check_even(number)
    if number % 2 == 0:
        print("Even number")
    else:
        print("Odd number")
endfunction

// Division by zero error
function divide_numbers(a, b)
    result = a / b
    print("Result is: ", result)
endfunction

// Corrected by adding a check for zero
function divide_numbers(a, b)
    if b != 0:
        result = a / b
        print("Result is: ", result)
    else:
        print("Error: Division by zero")
endfunction

// This loop will never execute
function print_numbers()
    for i=100 to 11
        print(i)
    next i
endfunction

// Corrected loop range
function print_numbers()
    for i=0 to 10
        print(i + 1)
    next i
endfunction

// Using a variable before it is declared
print(total)
total = 100

// Corrected by declaring the variable first
total = 100
print(total)

Trace Tables

- A trace table is a table that shows the steps taken to solve a problem.
- It is used to test algorithms and programs to make sure that there are no logical errors.
- Each step of the program is listed in the table, and they have columns for when each variable changes.
- Trace tables are another way to visualise the step-by-step execution of a program.

Example

01 | print("Numbers:")
02 | a = int(input())
03 | b = int(input())
04 | sum = 0
05 | while b > 0:
06 |   if b % 2 == 1:
07 |     sum = sum + a 
08 |   a = 2*a
09 |   b = b // 2
10 | print(sum)
        

And here is the trace table (assuming the input is 11 and 7):